Metacognitive Strategies

Metacognitive strategies empower students to think critically about their own learning processes, fostering self-awareness and control over problem-solving․ These strategies include self-monitoring, self-questioning, and reflective thinking, enabling students to evaluate their understanding and adjust their approaches as needed․

Teachers can model these strategies through think-alouds and explicit instruction, guiding students to articulate their thoughts and identify areas for improvement․ By encouraging students to plan, monitor, and reflect on their work, metacognition enhances problem-solving skills and mathematical confidence, making it a cornerstone of high-impact instructional practices in mathematics․

High-Impact Teaching Strategies in Mathematics

High-impact teaching strategies in mathematics include problem-solving, direct instruction, small-group work, and math conversations, fostering engagement and deeper understanding through structured, interactive, and student-centered approaches effectively․

Problem-Solving and Critical Thinking

Problem-solving and critical thinking are cornerstone strategies in high-impact mathematics instruction, enabling students to apply mathematical concepts to real-world scenarios․ These practices foster analytical reasoning, creativity, and logical thinking, preparing students for complex challenges․ By incorporating open-ended tasks and challenging questions, educators encourage students to explore multiple solutions, promoting deeper understanding and resilience․ Critical thinking is further cultivated through metacognitive strategies, where students reflect on their problem-solving processes, identifying strengths and areas for improvement․ This approach not only enhances math proficiency but also equips students with essential life skills․ Integrating problem-solving across math curricula ensures learners develop a robust foundation for tackling unfamiliar problems with confidence and precision․ Ultimately, these practices transform mathematics education into a dynamic, engaging, and intellectually stimulating experience․

Direct Instruction and Modeling

Direct instruction and modeling are highly effective strategies in mathematics education, providing students with clear, structured guidance; Teachers use explicit explanations, demonstrations, and step-by-step modeling to present mathematical concepts, ensuring clarity and reducing misconceptions․ This approach is particularly beneficial for introducing new skills or complex ideas, as it allows students to observe and imitate problem-solving processes․ Modeling also helps students understand the reasoning behind mathematical procedures, fostering deeper comprehension․ By combining direct instruction with opportunities for guided practice, educators create a supportive learning environment where students can apply what they’ve learned․ This method is especially valuable for building foundational skills and ensuring all learners have a solid grasp of key concepts before moving to independent practice․

Small-Group Instruction

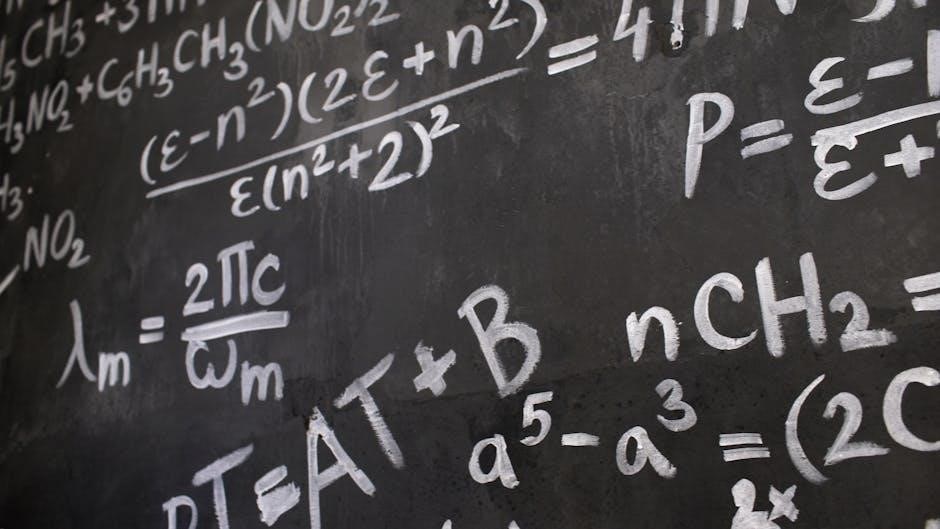
Small-group instruction is an effective strategy that involves dividing students into manageable groups to facilitate personalized learning and collaboration․ This approach allows teachers to tailor instruction to meet the diverse needs of students, ensuring that each learner receives targeted support․ In small groups, students can engage in peer discussions, work on problem-solving activities together, and receive immediate feedback from the teacher․ This collaborative environment not only enhances understanding of mathematical concepts but also encourages critical thinking and communication skills․ Additionally, small-group instruction can help identify and address individual learning gaps more efficiently, leading to improved academic outcomes in mathematics․

Math Conversations and Discourse

Math conversations and discourse are powerful tools for fostering deeper understanding and engagement in mathematics․ By encouraging students to articulate their thinking, teachers can promote critical thinking, communication, and problem-solving skills․ These discussions allow students to clarify misconceptions, explore multiple perspectives, and develop a stronger grasp of mathematical concepts․ When students engage in meaningful conversations about math, they learn to justify their reasoning, listen to others’ ideas, and refine their own understanding․ This collaborative approach creates a supportive learning environment where students feel confident sharing their thoughts․ Math discourse also enables teachers to assess student understanding in real-time, providing opportunities for targeted feedback and scaffolding․ Ultimately, fostering math conversations helps students develop a growth mindset and builds their confidence in tackling complex mathematical problems collaboratively․

Challenging Tasks and Open-Ended Questions

Challenging tasks and open-ended questions are essential for fostering critical thinking, creativity, and resilience in mathematics․ These tasks require students to explore problems from multiple angles, often without a single correct answer, encouraging deeper conceptual understanding․ Open-ended questions prompt students to justify their reasoning, communicate their thought processes, and consider alternative solutions․ Such approaches not only enhance problem-solving skills but also promote engagement and intellectual curiosity․ By incorporating challenging tasks, teachers can address diverse learning needs and cater to varying levels of student proficiency․ These strategies also prepare students for real-world scenarios where mathematical applications often involve complexity and uncertainty․ Ultimately, challenging tasks and open-ended questions empower students to develop a robust mathematical toolkit and apply it effectively to complex situations․

Feedback and Formative Assessment

Feedback and formative assessment are critical components of high-impact instructional practices in mathematics, enabling teachers to monitor student progress and adjust instruction accordingly․ Formative assessment involves ongoing, informal evaluations to gauge understanding, such as quizzes, exit tickets, or class discussions․ Feedback, whether verbal, written, or peer-based, provides students with specific insights to improve their performance․ These practices help identify learning gaps early, allowing for timely interventions and personalized support․ By incorporating feedback and formative assessment, teachers can create a data-driven classroom environment that fosters growth and accountability․ Students benefit from clear guidance, while teachers gain valuable insights to refine their instructional strategies․ This dynamic process ensures that learning is adaptive, engaging, and aligned with individual student needs, ultimately enhancing mathematical proficiency and confidence․

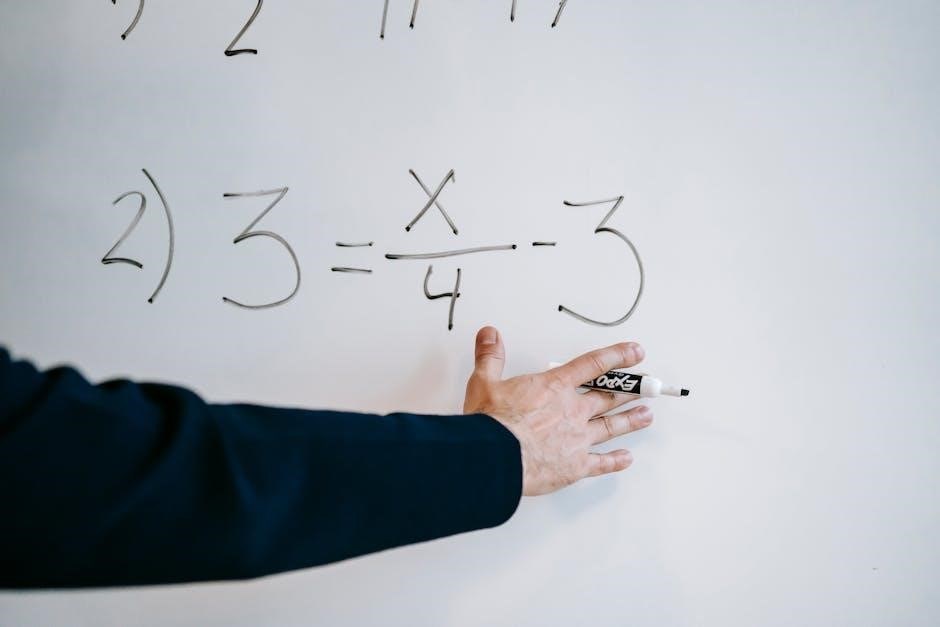
Technology Integration in Mathematics Education

Technology integration enhances math education by providing digital tools, interactive platforms, and real-time feedback, making abstract concepts engaging and accessible while supporting diverse learning needs effectively․

Digital Tools for Math Learning

Digital tools for math learning, such as interactive software, online platforms, and mobile apps, provide engaging and personalized experiences for students․ These tools often include virtual manipulatives, real-time feedback, and adaptive learning pathways that cater to individual needs․ They make complex mathematical concepts more accessible and visually understandable, promoting deeper comprehension․ Interactive simulations, for example, allow students to experiment with geometric shapes or algebraic equations in a dynamic environment․ Additionally, digital tools facilitate collaboration through shared workspaces and peer discussions, fostering a sense of community in math education․ By integrating these resources, educators can create a blended learning environment that supports diverse learning styles and enhances student motivation and achievement in mathematics․

Interactive Math Software and Apps

Interactive math software and apps are powerful resources that transform traditional learning into dynamic, engaging experiences․ These tools often feature interactive exercises, games, and real-time feedback, allowing students to explore mathematical concepts at their own pace․ Many platforms incorporate gamification elements, such as points, badges, and leaderboards, to motivate learners and make math practice enjoyable․ Interactive software also provides personalized learning paths, adapting to each student’s strengths and areas for improvement․ Additionally, these tools often include multimedia elements, such as animations and videos, to help visualize complex ideas․ By leveraging technology, interactive math software and apps create a flexible and inclusive learning environment that supports diverse learning styles and enhances student engagement and understanding in mathematics․ They are particularly effective for reinforcing skills and preparing for assessments․

Gamification of Math Concepts

Gamification of math concepts involves integrating game design elements into learning activities to enhance engagement and motivation․ By transforming mathematical problems into interactive and competitive experiences, students develop a more positive attitude toward math․ Points, badges, and leaderboards encourage progress tracking, while puzzles, challenges, and rewards make learning fun and dynamic․ Gamification also promotes active participation, allowing students to explore concepts in a low-stakes environment․ Real-time feedback helps students identify errors and improve their understanding․ Math-based games and simulations can be tailored to different skill levels, ensuring accessibility for all learners․ This approach not only fosters problem-solving skills but also builds confidence and perseverance․ By making math enjoyable and interactive, gamification creates a supportive and inclusive learning atmosphere that caters to diverse learning styles and preferences, ultimately enhancing mathematical proficiency and enthusiasm․ It is a modern and effective way to make math education more engaging and impactful․

Assessment and Data-Driven Instruction

Assessment and data-driven instruction are crucial for identifying student strengths and weaknesses, enabling teachers to tailor their methods and systematically improve mathematical outcomes effectively in classrooms․

Formative Assessments in Math

Formative assessments are crucial tools for monitoring student progress and understanding in mathematics․ These ongoing evaluations help identify strengths, weaknesses, and misconceptions, enabling teachers to adjust instruction․ Techniques include exit tickets, quizzes, class discussions, and observation of student work․ Unlike summative assessments, formative assessments are informal and occur during the learning process․ They promote engagement and provide immediate feedback, allowing students to reflect on their learning․ Teachers use this data to differentiate instruction, address gaps, and reinforce key concepts․ Regular formative assessments foster a growth mindset and improve problem-solving skills․ They also encourage collaboration and communication among students, enhancing their mathematical reasoning․ By integrating formative assessments, educators create a supportive environment tailored to individual needs, ensuring all students have opportunities to succeed in math․ This approach is vital for fostering long-term mathematical proficiency and confidence․

Summative Assessments and Their Role

Summative assessments are comprehensive evaluations used to measure student learning at the end of an instructional period, such as a unit, semester, or year․ These assessments provide a clear picture of whether students have achieved the desired learning outcomes․ They often take the form of final exams, projects, or standardized tests․ Summative assessments are crucial for accountability, as they help educators, parents, and administrators understand student performance․ They also inform decisions about grade promotion, curriculum adjustments, and future instructional strategies․ While they are less frequent than formative assessments, summative evaluations are essential for validating the effectiveness of teaching methods and ensuring alignment with educational standards․ By synthesizing data from summative assessments, educators can refine their practices and better support student success in mathematics․ These assessments play a key role in maintaining academic rigor and accountability in math education․ They are indispensable for tracking long-term progress and achievements․

Using Data to Inform Instruction

Using data to inform instruction is a cornerstone of high-impact teaching practices in mathematics․ By analyzing formative and summative assessment results, educators can identify patterns, strengths, and areas where students may need additional support․ This data-driven approach allows teachers to tailor their instruction to meet the specific needs of their students, ensuring that no learner falls behind․ For instance, if data shows a class struggles with fractions, the teacher can allocate more time to this topic or incorporate targeted interventions․ Data also helps in tracking progress over time, enabling educators to refine their strategies and improve academic outcomes․ By leveraging data effectively, teachers can create personalized learning experiences, fostering student confidence and mathematical proficiency․ This practice ensures that instruction is intentional, impactful, and aligned with student needs, ultimately enhancing overall learning outcomes in mathematics․

Creating a Supportive Mathematics Learning Environment

A supportive mathematics learning environment fosters engagement and understanding by encouraging growth mindsets, math discourse, and the use of visual representations to enhance problem-solving effectively․

Building a Growth Mindset

Building a growth mindset in mathematics education is crucial for fostering resilience and confidence in students․ It emphasizes that abilities and intelligence can be developed through effort, persistence, and dedication․ Teachers can cultivate this mindset by praising effort rather than just results, encouraging problem-solving discussions, and providing constructive feedback․ By framing challenges as opportunities for growth, students learn to embrace difficulties and view setbacks as stepping stones to success․ This approach helps students develop a positive attitude toward math, reducing anxiety and increasing engagement․ A growth mindset also promotes critical thinking and creativity, as students become more willing to explore and learn from their mistakes․ Ultimately, it empowers students to take ownership of their learning journey, leading to improved academic outcomes and lifelong mathematical proficiency․

Culturally Responsive Math Teaching

Culturally responsive math teaching involves creating an inclusive learning environment that values and integrates students’ diverse backgrounds, experiences, and perspectives․ This approach recognizes that mathematics is a universal language but acknowledges the cultural contexts in which it is learned․ Teachers can foster equity by using real-world examples that reflect students’ lives, incorporating diverse mathematical contributions from various cultures, and encouraging discussions that honor multiple problem-solving strategies․ By connecting math to students’ identities, educators can enhance engagement and motivation․ Culturally responsive practices also involve addressing implicit biases and ensuring all students feel seen and valued; This approach not only promotes academic success but also helps students develop a deeper appreciation for the relevance of math in their lives and in the broader society․

Differentiated Instruction in Math

Differentiated instruction in math tailors teaching methods to meet the diverse needs of all students, ensuring each learner receives appropriate challenges and support․ This approach recognizes that students vary in their learning styles, pacing, and understanding․ Teachers use strategies such as tiered assignments, learning centers, and technology to cater to individual differences․ By modifying content, process, and products, educators create multiple pathways for students to achieve learning goals․ Differentiated instruction fosters engagement, confidence, and a deeper understanding of mathematical concepts․ It also helps identify and address gaps in knowledge, allowing teachers to provide targeted interventions․ This inclusive approach ensures that all students, regardless of their ability level, feel valued and supported in their mathematical journey․ Ultimately, it promotes equity and excellence in math education by addressing the unique needs of every learner․

High-impact instructional practices in mathematics empower educators to create engaging, effective learning environments․ By integrating evidence-based strategies, teachers can foster student growth and mastery of mathematical concepts, ensuring long-term success․

Implementing High-Impact Practices Effectively

To implement high-impact instructional practices effectively, educators must prioritize professional development, ensuring they are well-trained in evidence-based strategies․ Creating a supportive learning environment is crucial, with access to appropriate resources and materials․ Collaboration among teachers fosters shared understanding and consistency in applying these practices․ Regular use of formative assessments allows for data-driven instruction, enabling timely interventions for students who need extra support․ Consistency in applying these practices is key to achieving long-term improvements in student outcomes․ By integrating feedback mechanisms and continuously refining teaching methods, educators can maximize the effectiveness of high-impact practices, ultimately enhancing student engagement, understanding, and mathematical proficiency․